Институт цветных металлов и золота СФУ
Кафедра автоматизации производственных процессов
Типы фильтров ФНЧ Баттерворта ФНЧ Чебышева I типа Минимальный порядок фильтра ФНЧ с МОС
ФНЧ на ИНУН Биквадратные ФНЧ Настройка фильтров 2 порядка ФНЧ нечетного порядка
ФНЧ Чебышева II типа Эллиптические ФНЧ Эллиптические ФНЧ на ИНУН Эллиптические ФНЧ на 3 конденсаторах Биквадратные эллиптические ФНЧ Настройка ФНЧ Чебышева II типа и эллиптических
Настройка фильтров 2 порядка Всепропускающие фильтры Моделирование ФНЧ Создание схем
Расчет переходных х-к Расчет частотных х-к Выполнение работы Контрольные вопросы
Лабораторная работа № 1
”Изучение фильтрация сигналов в среде Micro-Cap 6/7”
Цель работы
1. Изучить основные типы и характеристики фильтров
2. Исследовать моделирование фильтров в среде Micro-Cap 6.
3. Исследовать характеристики активных фильтров в среде Micro-Cap 6
Теоретические сведения
1. Типы и характеристики фильтров
Фильтрация сигналов играет важную роль в цифровых системах управления. В них фильтры используются для устранения случайных ошибок измерения (наложения сигналов помех, шумов) (рис. 1.1). Различают аппаратную (схемную) и цифровую (программную) фильтрацию. В первом случае используют электронные фильтры из пассивных и активных элементов, во втором случае применяют различные программные методы выделения и устранения помех. Аппаратная фильтрация применяется в модулях УСО (устройств связи с объектом) контроллеров и распределенных систем сбора данных и управления.
Цифровая фильтрация используется в УВМ верхнего уровня АСУ ТП. В данной работе подробно рассматриваются вопросы аппаратной фильтрации.
Различают следующие типы фильтров:фильтры нижних частот - ФНЧ (пропускают низкие частоты и задерживают высокие частоты);
фильтры верхних частот (пропускают высокие частоты и задерживают низкие частоты);
полосно-пропускающие фильтры (пропускают полосу частот и задерживают частоты, расположенные выше и ниже этой полосы);
полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).
Передаточная функция (ПФ) фильтра имеет вид:
где ½Н (j w)½- модуль ПФ или АЧХ; j (w) - ФЧХ; w - угловая частота (рад/с), связанная с частотой f (Гц) соотношением w = 2p f .
П Ф реализуемого фильтра имеет вид
где а и b - постоянные величины, а т , n = 1, 2, 3 ... (m £ n ).
Степень полинома знаменателя n определяет порядок фильтра. Чем он выше, тем лучше АЧХ, но сложнее схема, а стоимость выше.
Диапазоны или полосы частот, в которых сигналы проходят, - это полосы пропускания и в них значение АЧХ ½Н (j w)½ велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, - это полосы задерживания и в них значение АЧХ мало, а в идеальном случае равно нулю.
АЧХ реальных фильтров отличаются от теоретических АЧХ. Для ФНЧ идеальная и реальная АЧХ приведены на рис. 1.6.В реальных фильтрах полоса пропускания - это диапазон частот (0 - c), где значение АЧХ больше заданной величины А 1 . Полоса задерживания - это диапазон частот ( 1 -∞), в котором АЧХ меньше значения - A 2 . Интервал частот перехода от полосы пропускания к полосе задержания, ( c - 1) называют переходной областью.
Зачастую для характеристики фильтров вместо амплитуды используют затухание. Затухание в децибелах (дБ) определяют по формуле
Значению амплитуды А = 1 соответствует затухание a
= 0. Если A 1 = A/ = 1/=
0,707, то затухание на частоте w c:
= 1/=
0,707, то затухание на частоте w c:
|
Рис. 1.8. ФНЧ (а ) и его АЧХ (б ) |
На низких частотах (ниже 0,5 МГц), параметры катушек индуктивности неудовлетворительны: большие размеры и отклонения характеристик от идеальных. Катушки индуктивности плохо приспособлены для интегрального исполнения. Простейший фильтр низких частот (ФНЧ) и его АЧХ показаны на рис. 1.8.
Активные фильтры создаются на основе R , C элементов и активных элементов - операционных усилителей (ОУ). ОУ должны иметь: высокий коэффициент усиления (в 50 раз больше, чем у фильтра); высокую скорость нарастания выходного напряжения (до 100-1000 В/мкс).
|
Рис. 1.9. Т- и П-образные ФНЧ |
Фильтр четного порядка с п > 2 содержит n /2 звеньев второго порядка, соединенных каскадно. Фильтр нечетного порядка с п > 2 содержит (п – 1)/2 звеньев второго порядка и одно звено первого порядка.
Для фильтров первого порядка ПФ
где В и С - постоянные числа; P (s ) - полином второй или меньшей степени.
У ФНЧ максимальное затухание в полосе пропускания a 1 не превышает 3 дБ, а затухания в полосе задерживания a 2 находится в пределах от 20 до 100 дБ. Коэффициент усиления ФНЧ это значение его передаточной функции при s = 0 или значение его АЧХ при w = 0 , т.е. равен А.
Различают следующие типы ФНЧ:Баттерворта - обладают монотонной АЧХ (рис. 1.12);
Чебышева (типа I) - АЧХ содержит пульсации в полосе пропускания и монотонна в полосе задерживания (рис. 1.13);
инверсные Чебышева (типа II) - АЧХ монотонна в полосе пропускания и обладает пульсациями в полосе задерживания (рис. 1.14);
эллиптические - АЧХ имеет пульсации как в полосе пропускания, так и в полосе задерживания (рис. 1.15).
Фильтр Баттерворта НЧ n -го порядка имеет АЧХ следующего вида
ПФ фильтра Баттерворта как полиномиального фильтра равна
Для п = 3, 5, 7 ПФ нормированного фильтра Баттерворта равна
где параметры e и К - постоянные числа, а С п - полином Чебышева первого рода степени п , равный
Размах R р можно уменьшить, выбрав значение параметра e достаточно малым.
Минимально допустимое затухание в полосе пропускания - постоянный размах пульсаций - выражается в децибелах как
| |||
ПФ фильтров НЧ Чебышева и Баттерворта идентичны по форме и описываются выражениями (1.15) - (1.16). АЧХ фильтра Чебышева лучше АЧХ фильтра Баттерворта такого же порядка, т. к. у первого уже ширина переходной области. Однако у фильтра Чебышева ФЧХ хуже (более нелинейна) чем ФЧХ у фильтра Баттерворта.
АЧХ фильтра Чебышева данного порядка лучше АЧХ Баттерворта, так как у фильтра Чебышева уже ширина переходной области. Однако ФЧХ фильтра Чебышева хуже (более нелинейна) по сравнению с ФЧХ фильтра Баттерворта.
ФЧХ фильтра Чебышева для 2-7-го порядков приведены на рис. 1.18. Для сравнения на рис. 1.18 штриховой линией изображена ФЧХ фильтра Баттерворта шестого порядка. Можно также отметить, что ФЧХ фильтров Чебышева высокого порядка хуже ФЧХ фильтров более низкого порядка. Это согласуется с тем фактом, что АЧХ фильтра Чебышева высокого порядка лучше АЧХ фильтра более низкого порядка.
1.1. ВЫБОР МИНИМАЛЬНОГО ПОРЯДКА ФИЛЬТРА
На основе рис. 1.8 и 1.9 можно сделать вывод, что чем выше порядок фильтров Баттерворта и Чебышева, тем лучше их АЧХ. Однако более высокий порядок усложняет схемную реализацию и вследствие этого повышает стоимость. Таким образом, важен выбор минимально необходимого порядка фильтра, удовлетворяющего заданным требованиям.
Пусть в изображенной на рис. 1.2 общей характеристике заданы максимально допустимое затухание в полосе пропускания a 1 (дБ), минимально допустимое затухание в полосе задерживания a 2 (дБ), частота среза w с (рад/с) или f c (Гц) и максимальная допустимая ширина переходной области T W , которая определяется следующим образом:
где логарифмы могут быть или натуральными, или десятичными.
Уравнение (1.24) можно записать в виде
w с /w 1 = (T W / w с) + 1 |
и полученное соотношение подставить в (1.25) для нахождения зависимости порядка п от ширины переходной области, а не от частоты w 1 . Параметр T W / w с называется нормированной шириной переходной области и является безразмерной величиной. Следовательно, T W и w с можно задавать и в радианах на секунду, и в герцах.
Подобным же образом на основе (1.18) для К = 1 найдем минимальный порядок фильтра Чебышева
а из (1.25) следует, что удовлетворяющий этим требованиям фильтр Баттерворта должен иметь следующий минимальный порядок:
Снова находя ближайшее большее целое число, получаем п = 4.
Этот пример наглядно иллюстрирует преимущество фильтра Чебышева над фильтром Баттерворта, если основным параметром является АЧХ. В рассмотренном случае фильтр Чебышева обеспечивает ту же самую крутизну передаточной функции, что и фильтр Баттерворта удвоенной сложности.
1.2. ФНЧ С МНОГОПЕТЛЕВОЙ ОБРАТНОЙ СВЯЗЬЮ
И БЕСКОНЕЧНЫМ КОЭФФИЦИЕНТОМ УСИЛЕНИЯ
|
Рис. 1.11. ФНЧ с МОС второго порядка |
Для фильтров более высокого порядка уравнение (1.29) описывает ПФ типового звена второго порядка, где К – коэффициент его усиления; В и С – коэффициенты звена, приведенные в справочной литературе . Одна из наиболее простых схем активных фильтров, реализующих ПФ нижних частот согласно (1.29), приведена на рис. 1.11.
Эта схема реализует уравнение (1.29) с инвертирующим коэффициентом усиления – К (К > 0) иСопротивления, удовлетворяющие уравнению (1.30), равны
Целесообразный подход состоит в том, чтобы задать номинальное значение емкости C 2 , близкое к значению 10/f c мкФ и выбрать наибольшее имеющееся номинальное значение емкости C 1 , удовлетворяющее уравнению (1.31). Сопротивления должны быть близки к значениям, вычисленным по (1.31). Чем выше порядок фильтра, тем более критичными являются эти требования. Если в наличии отсутствуют вычисленные номинальные значения сопротивлений, то следует отметить, что все значения сопротивлений можно домножить на общий коэффициент при условии, что значения емкостей делятся на тот же самый коэффициент.
В качестве примера предположим, что необходимо разработать фильтр Чебышева с МОС второго порядка с неравномерностью передачи 0,5 дБ, полосой пропускания 1000 Гц и коэффициентом усиления равным 2. В этом случае К = 2, w с = 2π (1000), а из приложения А находим, что В = 1,425625 и С=1,516203. Выбирая номинальное значение C 2 = 10/f c = 10/1000=0,01 мкФ = 10 -8 Ф, из (1.32) получаем
Теперь предположим, что необходимо разработать фильтр Баттерворта шестого порядка с МОС, частотой среза f c = 1000 Гц и коэффициентом усиления K = 8. Он будет состоять из трех звеньев второго порядка, каждое с ПФ, определяемой уравнением (2.1). Выберем коэффициент усиления каждого звена K = 2, что обеспечивает требуемый коэффициент усиления самого фильтра 2∙2∙2=8. Из приложения А для первого звена находим В = 0,517638 и С = 1. Снова выберем номинальное значение емкости С 2 = 0,01 мкФ и в этом случае из (2.21) найдем С 1 = 0,00022 мкФ. Зададим номинальное значение емкости С 1 = 200 пФ и из (2.20) найдем значения сопротивлений R 2 =139,4 кОм; R 1 =69,7 кОм; R 3 = 90,9 кОм. Два других звена рассчитываются аналогичным способом, а затем звенья соединяются каскадно для реализации фильтра Баттерворта шестого порядка.
Из-за своей относительной простоты фильтр с МОС является одним из наиболее популярных типов фильтров с инвертирующим коэффициентом усиления. Он обладает также определенными преимуществами, а именно хорошей стабильностью характеристик и низким выходным полным сопротивлением; таким образом, его можно сразу соединять каскадно с другими звеньями для реализации фильтра более высокого порядка. Недостаток схемы состоит в том, что невозможно достичь высокого значения добротности Q без значительного разброса значений элементов и высокой чувствительности к их изменению. Для достижения хороших результатов коэффициент усиления К
Скорректированная ФНЧ -фильтром . ... МОС -структурой, является возможность регулировки усиления и полосы фильтра при изменении номиналов минимального ... фильтра на микросхемах типа ... имеет тот же порядок величины, что и... классические фильтры Чебышева и Баттерворта , ...
В данной статье мы поговорим про фильтр Баттерворта, рассмотрим порядки фильтров, декады и октавы, подробно разберем фильтр низких частот Баттерворта третьего порядка с расчетом и схемой.
Введение
В устройствах, которые используют фильтры для формирования частотного спектра сигнала, например, в системах связи или управления, форма или ширина спада, также называемая «полосой перехода», для простого фильтра первого порядка может быть слишком длинной или необходимы широкие и активные фильтры, разработанные с более чем одним «заказом». Эти типы фильтров обычно известны как фильтры «высокого порядка» или «n- го порядка».
Порядок фильтров
Сложность или тип фильтра определяется «порядком» фильтров и зависит от количества реактивных компонентов, таких как конденсаторы или катушки индуктивности в его конструкции. Мы также знаем, что скорость спада и, следовательно, ширина полосы перехода зависит от порядкового номера фильтра и что для простого фильтра первого порядка он имеет стандартную скорость спада 20 дБ / декаду или 6 дБ / октава.
Тогда для фильтра, имеющего n- й порядковый номер, он будет иметь последующую скорость спада 20n дБ / декаду или 6n дБ / октаву. Таким образом:
- фильтр первого порядка имеет скорость спада 20 дБ / декаду (6 дБ / октава)
- фильтр второго порядка имеет скорость спада 40 дБ / декаду (12 дБ / октава)
- фильтр четвертого порядка имеет частоту спада 80 дБ / декада (24 дБ / октава) и т. д.
Фильтры высокого порядка, такие как третий, четвертый и пятый, обычно формируются путем каскадного объединения одиночных фильтров первого и второго порядка.
Например, два фильтра нижних частот второго порядка могут быть соединены каскадно для получения фильтра нижних частот четвертого порядка и так далее. Несмотря на то, что порядок фильтра, который может быть сформирован, не ограничен, при увеличении порядка увеличиваются его размер и стоимость, а также снижается его точность.
Декады и октавы
Последний комментарий о Декадах и Октавах . По шкале частот декада — это десятикратное увеличение (умножение на 10) или десятикратное уменьшение (деление на 10). Например, от 2 до 20 Гц представляют одну декаду, тогда как от 50 до 5000 Гц представляют две декады (от 50 до 500 Гц, а затем от 500 до 5000 Гц).
Октава — это удвоение (умножить на 2) или уменьшение в два раза (деление на 2) по шкале частот. Например, от 10 до 20 Гц представляет одну октаву, а от 2 до 16 Гц — это три октавы (от 2 до 4, от 4 до 8 и, наконец, от 8 до 16 Гц), каждый раз удваивая частоту. В любом случае, логарифмические шкалы широко используются в частотной области для обозначения значения частоты при работе с усилителями и фильтрами, поэтому важно понимать их.
Поскольку резисторы, определяющие частоту, все равны, как и конденсаторы, определяющие частоту, отсечка или угловая частота (ƒ C) для первого, второго, третьего или даже для фильтра четвертого порядка также должны быть равны и найдены, используя знакомое уравнение:

Как и в случае фильтров первого и второго порядка, фильтры верхних частот третьего и четвертого порядка формируются простым взаимным обменом положений определяющих частоту компонентов (резисторов и конденсаторов) в эквивалентном фильтре нижних частот. Фильтры высокого порядка можно спроектировать, следуя процедурам, которые мы видели ранее в руководствах по фильтру нижних частот и фильтрам верхних частот. Однако общий коэффициент усиления фильтров высокого порядка является фиксированным, поскольку все компоненты, определяющие частоту, являются одинаковыми.
Аппроксимации фильтра
До сих пор мы рассматривали низкочастотные и высокочастотные схемы фильтра первого порядка, их результирующие частотные и фазовые характеристики. Идеальный фильтр дал бы нам спецификации максимального усиления полосы пропускания и плоскостности, минимального затухания полосы пропускания, а также очень крутой полосы пропускания, чтобы остановить спад полосы (полоса перехода), и поэтому очевидно, что большое количество сетевых откликов будет удовлетворять эти требования.
Неудивительно, что в линейном дизайне аналоговых фильтров есть ряд «аппроксимационных функций», в которых используется математический подход для наилучшего приближения передаточной функции, которая требуется нам для проектирования фильтров.
Такие конструкции известны как Эллиптический , Баттерворт , Чебышев , Бессель , Кауэр и многие другие. Из этих пяти «классических» функций аппроксимации линейного аналогового фильтра только фильтр Баттерворта и особенно конструкция фильтра Баттерворта нижних частот будут рассматриваться здесь как его наиболее часто используемая функция.
Низкочастотный фильтр Баттерворта
Частотная характеристика аппроксимационной функции фильтра Баттерворта также часто называется «максимально плоской» (без пульсаций) характеристикой, поскольку полоса пропускания спроектирована так, чтобы иметь частотную характеристику, которая является настолько плоской, насколько это математически возможно, от 0 Гц (DC) до частоты среза -3 дБ без пульсаций. Более высокие частоты за пределами точки отсечки снижаются до нуля в полосе останова на уровне 20 дБ / декада или 6 дБ / октава. Это потому, что он имеет «фактор качества», «Q» всего 0,707.
Однако одним из основных недостатков фильтра Баттерворта является то, что он достигает этой плоскостности полосы пропускания за счет широкой полосы перехода, когда фильтр изменяется от полосы пропускания к полосе остановки. Он также имеет плохие фазовые характеристики. Идеальная частотная характеристика, называемая фильтром «кирпичной стены», и стандартные аппроксимации Баттерворта для различных порядков фильтра приведены ниже.

Обратите внимание, что чем выше порядок фильтра Баттерворта, тем больше количество каскадных ступеней в конструкции фильтра и тем ближе фильтр подходит к идеальному отклику «кирпичной стены».
Однако на практике идеальная частотная характеристика Баттерворта недостижима, поскольку она вызывает чрезмерную пульсацию в полосе пропускания.
Где обобщенное уравнение, представляющее фильтр Баттерворта «n-го» порядка, частотная характеристика дается как:

Где: n представляет порядок фильтра, ω равно 2πƒ, а ε — максимальное усиление полосы пропускания (A max).
Если A max определено на частоте, равной угловой точке отсечки -3 дБ (ƒc), тогда ε будет равно единице и, следовательно, ε 2 также будет равно единице. Однако, если вы теперь хотите определить A max при другом значении усиления по напряжению, например, 1 дБ или 1.1220 (1 дБ = 20 * logA max), тогда новое значение ε находится по формуле:

Подставляя данные в уравнения, получаем:

Частотная характеристика фильтра может быть определена математически его передаточной функции с стандартом передачи напряжения Функция H (jω) и записывается в виде:

Примечание: (jω) также можно записать как (s) для обозначения S-области. и результирующая передаточная функция для фильтра нижних частот второго порядка задается как:

Нормализованные полиномы фильтра Баттерворта низких частот
Чтобы помочь в разработке своих фильтров нижних частот, Баттерворт создал стандартные таблицы нормализованных полиномов нижних частот второго порядка с учетом значений коэффициента, которые соответствуют частоте отсечки угла 1 радиан / с.
| N | Нормализованные полиномы знаменателя в факторизованной форме |
| 1 | (1 + S) |
| 2 | (1 + 1,414 с + с 2) |
| 3 | (1 + с) (1 + с + с 2) |
| 4 | (1 + 0,765 с + с 2) (1 + 1,848 с + с 2) |
| 5 | (1 + с) (1 + 0,618 с + с 2) (1 + 1,618 с + с 2) |
| 6 | (1 + 0,518 с + с 2) (1 + 1,414 с + с 2) (1 + 1,932 с + с 2) |
| 7 | (1 + с) (1 + 0,445 с + с 2) (1 + 1,247 с + с 2) (1 + 1,802 с + с 2) |
| 8 | (1 + 0,390 с + с 2) (1 + 1,111 с + с 2) (1 + 1,663 с + с 2) (1 + 1,962 с + с 2) |
| 9 | (1 + с) (1 + 0,347 с + с 2) (1 + с + с 2) (1 + 1,532 с + с 2) (1 + 1,879 с + с 2) |
| 10 | (1 + 0,313 с + с 2) (1 + 0,908 с + с 2) (1 + 1,414 с + с 2) (1 + 1,782 с + с 2) (1 + 1,975 с + с 2) |
Расчет и схема фильтра Баттерворта низких частот
Найти порядок активного фильтра Баттерворта нижних частот, чьи характеристики приведены в качестве: A макс = 0,5 дБ на частоте полосы пропускания (ωp) 200 радиан / сек (31.8 гЦ), и A min = -20 дБ на частоте полосы остановки (ωs) 800 радиан / сек. Также разработайте подходящую схему фильтра Баттерворта, соответствующую этим требованиям.
Во-первых, максимальное усиление полосы пропускания A max = 0,5 дБ, которое равно усилению 1,0593 , помните, что: 0,5 дБ = 20 * log (A) на частоте (ωp) 200 рад / с, поэтому значение эпсилона ε находится по:

Во-вторых, минимальное усиление полосы остановки A min = -20 дБ, которое равно усилению 10 (-20 дБ = 20 * log (A)) на частоте полосы остановки (ωs) 800 рад / с или 127,3 Гц.
Подстановка значений в общее уравнение для частотной характеристики фильтров Баттерворта дает нам следующее:

Так как n всегда должно быть целым числом, то следующим самым высоким значением 2,42 будет n = 3 , поэтому «требуется фильтр третьего порядка», и для создания фильтра Баттерворта третьего порядка, ступени фильтра второго порядка требуется каскадное соединение со ступенью фильтра первого порядка.
Из приведенной выше таблицы нормализованных полиномов Баттерворта низких частот коэффициент для фильтра третьего порядка дается как (1 + s) (1 + s + s 2), и это дает нам усиление 3-A = 1 или A = 2 . В А = 1 + (Rf / R1) , выбирая значение как для резистора обратной связи Rf и резистора R1 дает нам значения 1 кОм и 1 кОм, соответственно, как: (1 кОм / 1 кОм) + 1 = 2 .
Мы знаем, что угловая частота отсечки, точка -3 дБ (ω o) может быть найдена с помощью формулы 1 / CR , но нам нужно найти ω o по частоте полосы пропускания ω p ,

Таким образом, частота отсечки угла задается как 284 рад / с или 45,2 Гц (284 / 2π), и, используя знакомую формулу 1 / RC, мы можем найти значения резисторов и конденсаторов для нашей схемы третьего порядка.

Обратите внимание, что ближайшее предпочтительное значение до 0,352 мкФ будет 0,36 мкФ или 360 нФ.
И, наконец, наша схема низкочастотного фильтра Баттерворта третьего порядка с угловой частотой среза 284 рад / с или 45,2 Гц, максимальным усилением полосы пропускания 0,5 дБ и минимальным усилением полосы остановки 20 дБ строится следующим образом.

Таким образом, для нашего фильтра низких частот Баттерворта 3-го порядка с угловой частотой 45,2 Гц, C = 360 нФ и R = 10 кОм
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)

Фильтр Баттерворта 4 порядка

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)

Фильтр Чебышева 3 порядка

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)


ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)
Фильтр Чебышева 4 порядка
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)


ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)

Фильтр Бесселя 3 порядка
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)

Фильтр Бесселя 4 порядка
ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФНЧ1)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ФВЧ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> ПФ)

ПРЕОБРАЗОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЦФ (ФНЧ --> РФ)

Произвести анализ влияния ошибок задания коэффициентов цифрового ФНЧ на АЧХ (изменяя один из коэффициентов b j ). Описать характер изменения ЧХ. Сделать вывод о влиянии изменения одного из коэффициентов на поведение фильтра.
Анализ влияния ошибок задания коэффициентов цифрового ФНЧ на АЧХ проведем на примере фильтра Бесселя 4 порядка.
Выберем величину отклонения коэффициентов ε, равной –1,5%, чтобы максимальное отклонение АЧХ составило около 10%.
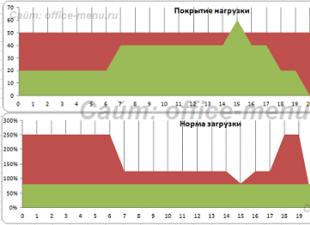
АЧХ "идеального" фильтра и фильтров с измененными коэффициентами на величину ε показана на рисунке:

И
 з
рисунка видно, что наибольшее влияние
на АЧХ оказывает изменение коэффициентовb 1
и b 2 ,
(их величина превышает величину других
коэффициентов). Используя отрицательную
величину ε, отмечаем, что положительные
коэффициенты уменьшают амплитуду в
нижней части спектра, а отрицательные
– увеличивают. При положительной
величине ε, все происходит наоборот.
з
рисунка видно, что наибольшее влияние
на АЧХ оказывает изменение коэффициентовb 1
и b 2 ,
(их величина превышает величину других
коэффициентов). Используя отрицательную
величину ε, отмечаем, что положительные
коэффициенты уменьшают амплитуду в
нижней части спектра, а отрицательные
– увеличивают. При положительной
величине ε, все происходит наоборот.
Проквантовать коэффициенты цифрового фильтра на такое число двоичных разрядов, чтобы максимальное отклонение АЧХ от исходной составляло порядка 10 - 20%. Зарисовать АЧХ и описать характер ее изменения.
Изменяя число разрядов дробной части коэффициентов b j отметим, чтомаксимальное отклонение АЧХ от исходной не превышающее 20% получается приn≥3.
Вид АЧХ при различных n приведен на рисунках:
n =3, максимальное отклонение АЧХ=19,7%

n =4, максимальное отклонение АЧХ=13,2%

n =5, максимальное отклонение АЧХ=5,8%

n =6, максимальное отклонение АЧХ=1,7%

Таким образом, можно отметить, что увеличение разрядности при квантовании коэффициентов фильтра приводит к тому, что АЧХ фильтра все больше стремится к исходной. Однако необходимо отметить, что это усложняет физическую реализуемость фильтра.
Квантование при различных n можно проследить по рисунку:

План:
-
Введение
- 1
Обзор
- 1.1 Нормированные полиномы Баттерворта
- 1.2 Максимальная гладкость
- 1.3 Спад характеристики на высоких частотах
- 2
Проектирование фильтра
- 2.1 Топология Кауэра
- 2.2 Топология Саллена-Кея
- 3 Сравнение с другими линейными фильтрами
- 4 Пример Литература
Введение
Фильтр Баттерво́рта - один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания.
Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом в статье «О теории фильтрующих усилителей» (англ. On the Theory of Filter Amplifiers ), в журнале Wireless Engineer в 1930 году.
1. Обзор
АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления. В случае фильтра первого порядка АЧХ затухает со скоростью −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка - на −18 дБ и так далее. АЧХ фильтра Баттерворта - монотонно убывающая функция частоты. Фильтр Баттерворта - единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
В сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.
АЧХ для фильтров Баттерворта нижних частот порядка от 1 до 5. Наклон характерстики - 20n дБ/декаду, где n - порядок фильтра.
Как и для всех фильтров при рассмотрении частотных характеристик используют фильтр нижних частот, из которого легко можно получить фильтр высоких частот, а, включив несколько таких фильтров последовательно, - полосовой фильтр или режекторный фильтр.
Амплитудно-частотная характеристика фильтра Баттерворта -го порядка может быть получена из передаточной функции :
Легко заметить, что для бесконечных значений АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления , а частоты выше частоты среза будут полностью подавляться. Для конечных значений спад характеристики будет пологим.
С помощью формальной замены представим выражение в виде :
Полюсы передаточной функции расположены на круге радиуса равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости. -й полюс определяется из следующего выражения:
Передаточную функцию можно записать в виде:
Аналогичные рассуждения применимы и к цифровым фильтрам Баттерворта, с той лишь разницей, что соотношения записываются не для s -плоскости, а для z -плоскости.
Знаменатель этой передаточной функции называется полиномом Баттерворта.
1.1. Нормированные полиномы Баттерворта
Полиномы Баттерворта могут записываться в комплексной форме, как показано выше, однако обычно они записываются в виде соотношений с вещественными коэффициентами (комплексно-сопряжённые пары объединяются с помощью умножения). Нормируются полиномы по частоте среза: . Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:
, - чётно , - нечётноНиже представлены коэффициенты полиномов Баттерворта для первых восьми порядков:
|
1.2. Максимальная гладкость
Приняв и , производная амплитудной характеристики по частоте будет выглядеть следующим образом:
Она монотонно убывает для всех так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристи в ряд, получим:
Другими словами, все производные амплитудно-частотной характерситики по частоте до 2n -й равны нулю, из чего следует «максимальная гладкость».
1.3. Спад характеристики на высоких частотах
Приняв , найдём наклон логарифма АЧХ на высоких частотах:
В децибелах высокочастотная асимптота имеет наклон −20n дБ/декаду.
2. Проектирование фильтра
Существует ряд различных топологий фильтра, с помощью которых реализуются линейные аналоговые фильтры. Эти схемы отличаются только значениями элементов, структура же остаётся неизменной.
2.1. Топология Кауэра
Топология Кауэра использует пассивные элементы (ёмкости и индуктивности) . Фильтр Баттеворта с заданной передаточной функцией может быть построен в форме Кауэра 1 типа. k-й элемент фильтра задаётся соотношением:
; k нечётно ; k чётно2.2. Топология Саллена-Кея
Топология Саллена-Кея использует помимо пассивных также и активные элементы (операционные усилители и ёмкости). Каждый каскад схемы Саллена-Кея представляет собой часть фильтра, математически описываемую парой комплексно-сопряжённых полюсов. Весь фильтр получается последовательным соединением всех каскадов. В случае, если попадается действительный полюс, он должен быть реализован отдельно, обычно в виде RC-цепочки, и включён в общую схему.
Передаточная функция каждого каскада в схеме Саллена-Кея имеет вид:
Нужно, чтобы знаменатель представлял собой один из множителей полинома Баттерворта. Приняв , получим:
Последнее соотношение даёт две неизвестных, которые могут быть выбраны произвольно.
3. Сравнение с другими линейными фильтрами
Рисунок ниже показывает АЧХ фильтра Баттерворта в сравнении с другими популярными линейными фильтрами одинакового (пятого) порядка:
Из рисунка видно, что спад АЧХ фильтра Баттерворта самый медленный из четырёх, однако он имеет и самую гладкую АЧХ на частотах полосы пропускания.
4. Пример
Аналоговый фильтр Баттерворта нижних частот (топология Кауэра) с частотой среза со следующими номиналами элементов: фарад, ом, и генри.
Логарифмический график плотности передаточной функции H(s) на плоскости комплексного аргумента для фильтра Баттерворта третьего порядка с частотой среза . Три полюса лежат на круге единичного радиуса в левой полуплоскости.
Рассмотрим аналоговый низкочастотный фильтр Баттерворта третьего порядка с фарад, ом, и генри. Обозначив полное сопротивление ёмкостей C как 1/Cs и полное сопротивление индуктивностей L как Ls , где - комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:
АЧХ задаётся уравнением:
а ФЧХ задаётся уравнением:
Групповая задержка определяется как минус производная фазы по круговой частоте и является мерой искажений сигнала по фазе на различных частотах. Логарифмическая АЧХ такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.
График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.
Заменив каждую индуктивность ёмкостью, а ёмкости - индуктивностями, получим высокочастотный фильтр Баттерворта.
И групповая задержка фильтра Баттерворта третьего порядка с частотой среза
Литература
- В.А. Лукас Теория автоматического управления. - M.: Недра, 1990.
- Б.Х. Кривицкий Справочник по теоретическим основам радиоэлектроники. - М .: Энергия, 1977.
- Miroslav D. Lutovac Filter Design for Signal Processing using MATLAB© and Mathematica©. - New Jersey, USA.: Prentice Hall, 2001. - ISBN 0-201-36130-2
- Richard W. Daniels Approximation Methods for Electronic Filter Design. - New York: McGraw-Hill, 1974. - ISBN 0-07-015308-6
- Steven W. Smith The Scientist and Engineer’s Guide to Digital Signal Processing. - Second Edition. - San-Diego: California Technical Publishing, 1999. - ISBN 0-9660176-4-1
- Britton C. Rorabaugh Approximation Methods for Electronic Filter Design. - New York: McGraw-Hill, 1999. - ISBN 0-07-054004-7
- B. Widrow, S.D. Stearns Adaptive Signal Processing. - Paramus, NJ: Prentice-Hall, 1985. - ISBN 0-13-004029-0
- S. Haykin Adaptive Filter Theory. - 4rd Edition. - Paramus, NJ: Prentice-Hall, 2001. - ISBN 0-13-090126-1
- Michael L. Honig, David G. Messerschmitt Adaptive Filters - Structures, Algorithms, and Applications. - Hingham, MA: Kluwer Academic Publishers, 1984. - ISBN 0-89838-163-0
- J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. - New York: Springer-Verlag, 1982. - ISBN 0-387-07563-1
- L.R. Rabiner, R.W. Schafer Digital Processing of Speech Signals. - Paramus, NJ: Prentice-Hall, 1978. - ISBN 0-13-213603-1
- Richard J. Higgins Digital Signal Processing in VLSI. - Paramus, NJ: Prentice-Hall, 1990. - ISBN 0-13-212887-X
- A. V. Oppenheim, R. W. Schafer Digital Signal Processing. - Paramus, NJ: Prentice-Hall, 1975. - ISBN 0-13-214635-5
- L. R. Rabiner, B. Gold Theory and Application of Digital Signal Processing. - Paramus, NJ: Prentice-Hall, 1986. - ISBN 0-13-914101-4
- John G. Proakis, Dimitris G. Manolakis Introduction to Digital Signal Processing. - Paramus, NJ: Prentice-Hall, 1988. - ISBN 0-02-396815-X
1 Определим порядок фильтра. Порядок фильтра это число реактивных элементов в ФНЧ и ФВЧ.
где
 -
функция Баттерворта, соответствующая
допустимой частоте
-
функция Баттерворта, соответствующая
допустимой частоте .
.
 -
допустимое затухание.
-
допустимое затухание.
2 Чертим схему фильтра полученного порядка. При практической реализации предпочтительны схемы с меньшим количеством индуктивностей.
3 Рассчитываем постоянные преобразования фильтра.
 ,
мГн
,
мГн
 ,
нФ
,
нФ
4 Для идеального фильтра с сопротивлением
генератора 1 Ом, сопротивление нагрузки
1 Ом,
 составлена
таблица нормированных коэффициентов
фильтра Баттерворта. В каждой строке
таблицы коэффициенты симметричны, к
середине увеличиваются, а затем
уменьшаются.
составлена
таблица нормированных коэффициентов
фильтра Баттерворта. В каждой строке
таблицы коэффициенты симметричны, к
середине увеличиваются, а затем
уменьшаются.
5 Чтобы найти элементы схемы, необходимо постоянные преобразования умножить на коэффициент из таблицы.
|
Порядок фильтра |
Порядковые номера фильтра m |
|||||||||
Рассчитать параметры фильтра низких
частот Баттерворта, если ПП=0,15 кГц,
 =25
кГц,
=25
кГц, =30
дБ,
=30
дБ, =75
Ом. Найти
=75
Ом. Найти для трех точек.
для трех точек.
29.3 Фвч Баттерворта.
Фильтры ФВЧ – это четырехполюсники, у
кторых в диапазоне ( )
затухание мало, а в диапазоне (
)
затухание мало, а в диапазоне ( )
– велико, то есть фильтр должен пропускать
в нагрузку токи верхних частот.
)
– велико, то есть фильтр должен пропускать
в нагрузку токи верхних частот.

Так как ФВЧ должен пропускать токи высоких частот, то на пути тока, идущего в нагрузку, должен стоять частотно зависимый элемент, который хорошо пропускает токи высоких частот и плохо токи низких частот. Таким элементом является конденсатор.
Ф ВЧ
Т-образный
ВЧ
Т-образный
ФВЧ П-образный
Конденсатор ставят последовательно с
нагрузкой, так как
 и с ростом частоты
и с ростом частоты уменьшается, следовательно токи высоких
частот легко проходят в нагрузку через
конденсатор. Катушку индуктивности
ставят параллельно нагрузке, так как
уменьшается, следовательно токи высоких
частот легко проходят в нагрузку через
конденсатор. Катушку индуктивности
ставят параллельно нагрузке, так как и с увеличением частоты увеличивается
и с увеличением частоты увеличивается ,
поэтому токи низких частот замыкаются
через индуктивности и не попадут в
нагрузку.
,
поэтому токи низких частот замыкаются
через индуктивности и не попадут в
нагрузку.
Расчет ФВЧ Баттерворта аналогичен расчету ФНЧ Баттерворта, проводится по тем же формулам, только



 .
.
Рассчитать фильтр верхних частот ФВЧ
Баттерворта, если
 Ом,
Ом, кГц,
кГц, дБ,
дБ, кГц.
Найти:
кГц.
Найти: .
.
Тема занятия 30: Полосовые и режекторные фильтры Баттерворта.
 sotikteam.ru Смартфоны. Антивирусы. Программы. Инструкции. Браузеры.
sotikteam.ru Смартфоны. Антивирусы. Программы. Инструкции. Браузеры.


 .
.